Description:
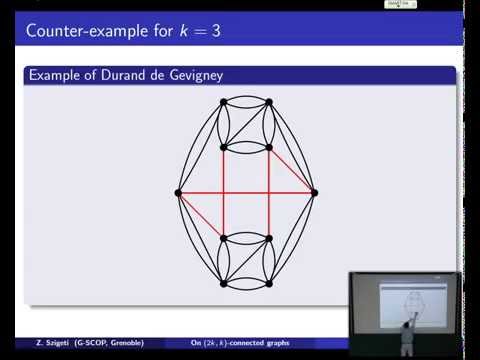
Explore a lecture on graph theory focusing on (2k,k)-connected graphs, presented by Zoltán Szigeti in collaboration with Olivier Durand de Gevigney. Delve into various aspects of graph connectivity, including arc-connectivity, k-vertex-connectivity, and edge-connectivity. Learn about orientation techniques for different types of connectivity, examine a counter-example for k=3, and understand construction methods for edge-connectivity and (4,2)-connectivity. Discover splitting off techniques for edge-connectivity and (4,2)-connectivity, and investigate a general method for (2k,k)-connected graphs. Gain insights into the orientation and proof of (2k,k)-connectivity in this comprehensive 47-minute talk, presented as part of the Hausdorff Trimester Program on Combinatorial Optimization.
Zoltán Szigeti: On -2k,k--connected Graphs
Add to list