Play all

Introduction

Time series data from sound recordings

Julia notebook: Playing with sound - WAV files

Drawing waveforms

Effect of frequency

Combining (superposing) different frequencies

Julia: FFT function

Discrete Fourier Transform (DFT) vs Fast Fourier Transform (FFT)

Plotting an FFT

Musical overtones: Magnitude of the FFT

Analyzing a sound file using the FFT

Defining the DFT mathematically

First term of the DFT

Visualizing the DFT in the complex plane

Equally-spaced points on unit circle in the complex plane

Idea of Fourier transform of a signal: walking around a circle

Adding complex numbers as adding vectors

Magnitude of DFT gives information about frequency

Angle of DFT gives information about phase

Interpreting the second term of the DFT

General formula for DFT

Implementing the DFT in Julia

Julia: Writing "i" as im

Julia: Array comprehension

Comparison of DFT with FFT results

Julia: isapprox for testing approximate equality

Efficiency of the implementation

Pre-computing an array of powers

Julia: Modulo (%)

Julia: OffsetArray for zero-based indexing

Computational complexity of DFT vs FFT

DFT as polynomials

Description:

Explore the Discrete Fourier Transform (DFT) in this 35-minute video lecture from MIT's 18.S191 Fall 2020 course. Dive into the fundamentals of DFT, its application in sound analysis, and its implementation using Julia programming language. Learn how to manipulate time series data from sound recordings, visualize waveforms, and understand the effects of frequency. Compare the Discrete Fourier Transform with the Fast Fourier Transform (FFT), plot FFTs, and analyze musical overtones. Discover the mathematical definition of DFT, visualize it in the complex plane, and grasp the concept of Fourier transform as a circular walk. Implement DFT in Julia, explore array comprehension, and compare DFT results with FFT. Gain insights into computational efficiency, pre-computing techniques, and the use of OffsetArrays for zero-based indexing. Conclude with an understanding of the computational complexity differences between DFT and FFT, and explore DFT as polynomials.

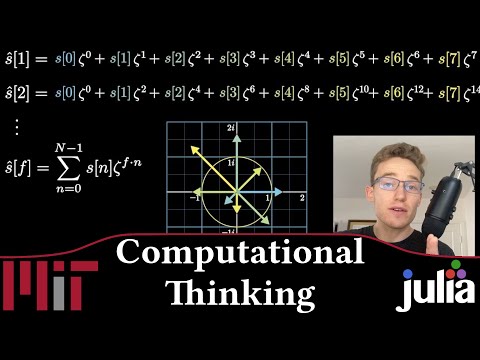
Understanding the Discrete Fourier Transform - Week 14

The Julia Programming Language

Add to list

#Engineering #Electrical Engineering #Signal Processing #Discrete Fourier Transforms #Computer Science #Algorithms #Computational Complexity #Mathematics #Complex Numbers #Fast Fourier Transform