Description:
Explore a rejuvenated algebraic approach to calculus in this 48-minute lecture on differential geometry. Delve into the powerful methods developed by Newton, Euler, and Lagrange, focusing on studying polynomial functions through translation and truncation to create Taylor approximations. Learn how to identify tangent lines, conics, and cubics for polynomials using only high school mathematics, without limits or real numbers. Compare this elementary theory to the standard textbook approach, and discover the advantages of using sub-derivatives instead of traditional derivatives. Work through explicit examples to gain practical understanding, and consider the potential impact of this perspective on mathematics education. Challenge conventional wisdom and adopt a beginner's mind to unlock new possibilities in this fundamental subject.
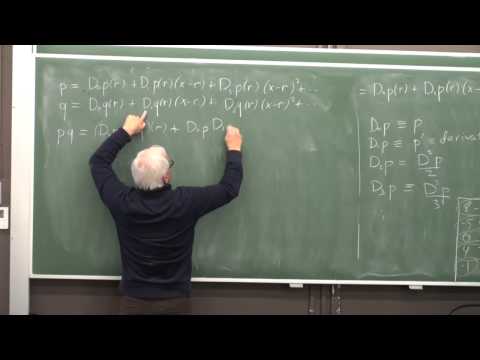
The Differential Calculus for Curves - Lagrange's Algebraic Approach - Lecture 4
Add to list
#Mathematics
#Geometry
#Differential Geometry
#Calculus
#Algebra
#Polynomial Functions
#Tangent Lines