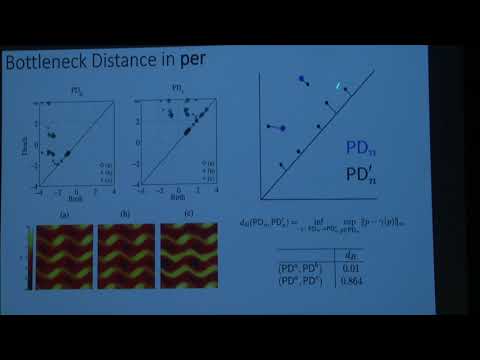
Explore the application of persistent homology in studying fluid flows through this comprehensive lecture. Delve into topics such as 2D Kolmogorov Flow, sublevel set persistent homology, and bottleneck distance in persistent homology. Examine the challenges of dealing with multiple time scales and learn about the Algebraic Stability Theorem for Generalized Interleavings. Investigate 2D Rayleigh-Bénard Convection, focusing on spiral defect chaos, Lyapunov vectors, and topological defects. Discover how persistent homology can be used to classify canonical patterns and identify critical point pairings. Explore the concept of persistent homology defects and the challenges of finding correspondences in persistence diagrams. Compare linear interpolation with actual flow in fluid dynamics. Extend the discussion to 3D Navier-Stokes equations and fully-developed turbulence, utilizing diffusion maps and landscape metrics. Uncover a new relationship in fluid dynamics and examine the Tsurushima Mechanism for HCCI. Conclude by learning how to differentiate chemical species using speed profiles and reaction profiles. Read more