Description:
Explore quantum projective spaces through a comprehensive lecture on split extensions and KK-equivalences. Delve into topics such as quantum homogeneous spaces, graph algebras, gauge actions, and complex projective lines. Examine the intricacies of KK Theory, KK-equivalences, and the UCT class. Investigate splitting homomorphisms, canonical maps, and the construction of KK equivalences. Learn about the UCT and its implications in this advanced mathematical discourse presented by Francesca Arici from Universiteit Leiden, Holland.
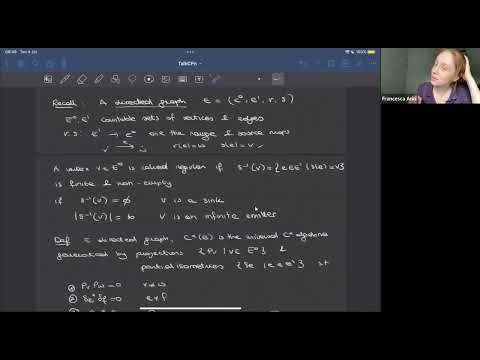
Spilt Extensions and KK-Equivalences for Quantum Projective Spaces
Add to list
#Mathematics
#Geometry
#Noncommutative Geometry
#C* algebras
#Art & Design
#Music
#Music Theory
#K Theory