Description:
Explore the intricate connections between Lie groups, singular chains, and Cartan relations in this mathematics seminar. Delve into the description of representations of C(G) using the differential graded Lie algebra Tg, and uncover its relationship to Chern-Weil theory and higher local systems on the classifying space BG. Learn about the group ring, singular chains, and an equivalence of categories. Examine the proof's key components, including Chen's iterated integrals, Bott-Shulman-Stasheff algebra, and the non-commutative Weil algebra. Investigate practical examples such as the trivial representation and the free loop space of BG to solidify understanding of these advanced mathematical concepts.
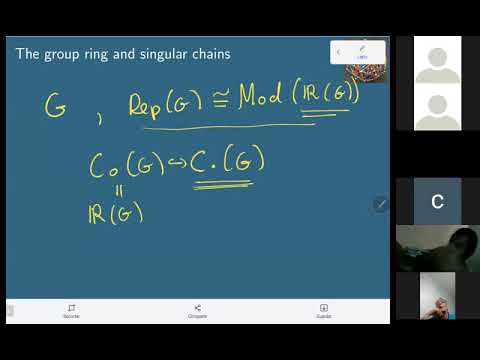
Singular Chains on Lie Groups and the Cartan Relations
Add to list