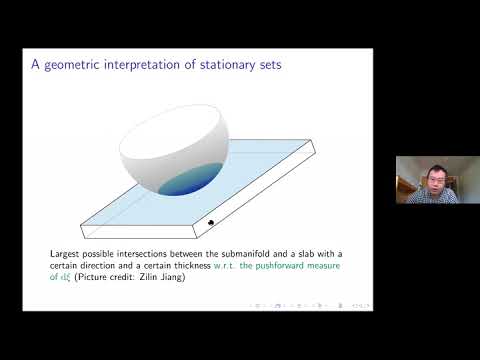
Explore a "stationary set" method for estimating oscillatory integrals in this 58-minute lecture by Ruixiang Zhang from the Hausdorff Center for Mathematics. Delve into the theory of o-minimal structures and discover how this approach provides an upper bound with simple geometric meaning. Learn about the application of this bound to obtain the sharp convergence exponent in the two-dimensional Tarry's problem for every degree. Examine the implications for sharp L∞→Lp Fourier extension estimates for two-dimensional Parsell-Vinogradov surfaces. Gain insights into topics such as one-parameter oscillation integrals, constructive interference, sublevel sets, number theory motivation, and semi-algebraic functions. Understand the conceptual proof involving semiaddress sets and slice volume functions in this joint work with Saugata Basu, Shaoming Guo, and Pavel Zorin-Kranich.