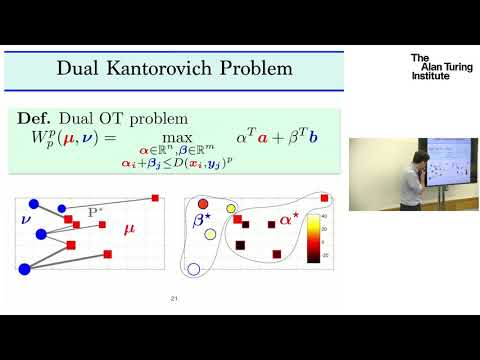
Explore the theoretical foundations of learning in this 44-minute conference talk focusing on regularization techniques for Optimal Transport and Dynamic Time Warping distances. Delve into the intersection of statistics, probability, and optimization as applied to structured mathematical objects like point clouds, histograms, and time series. Discover how early optimization methods, including linear and dynamic programming, have led to powerful distance metrics such as Wasserstein distances and dynamic time warping scores. Learn about two distinct smoothing strategies that improve these non-differentiable quantities for machine learning applications, with a focus on computing Fréchet means. Examine topics including dynamic time warping, pairwise distance matrices, alignment paths, Wasserstein distances for discrete measures, and the Kantorovich problem. Investigate the challenges of using DTW and OT as loss functions, and explore solutions like softmin of quadratic functions and recursive computations. Gain insights into fast and scalable algorithms, including the Sinkhorn algorithm, and understand their applications in interpolating between time series. Read more