Description:
Explore the connection between maximally monotone operators and convex functions in this 44-minute lecture by Regina Burachik. Delve into the concept of enlargements as a bridge between these mathematical entities, understanding their bijective correspondence with convex functions and their practical applications. Learn how enlargements provide insights into existing tools linked to convex functions and their role in defining distances between point-to-set maps. Examine topics such as inclusion problems, variational inequality problems, subdifferentials, and optimality conditions. Gain a comprehensive understanding of the theoretical foundations and practical implications of enlargements in mathematical analysis.
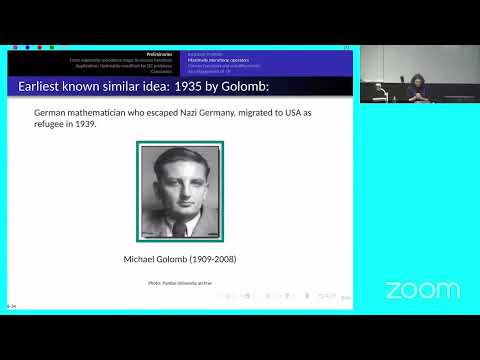
Enlargements - A Bridge Between Maximal Monotonicity and Convexity
Add to list