Play all

Real Analysis - Part 1 - Introduction

Real Analysis - Part 2 - Sequences and limits

Real Analysis - Part 3 - Bounded sequences and unique limits

Real Analysis - Part 4 - Theorem on limits

Real Analysis - Part 5 - Sandwich theorem

Real Analysis - Part 6 - Supremum and Infimum

Real Analysis - Part 7 - Cauchy sequences and Completeness

Real Analysis - Part 8 - Example Calculation

Real Analysis - Part 9 - Subsequences and accumulation values

Real Analysis - Part 10 - Bolzano-Weierstrass theorem

Real Analysis - Part 11 - Limit superior and limit inferior

Real Analysis - Part 12 - Examples for Limit superior and limit inferior

Real Analysis - Part 13 - Open, Closed and Compact Sets

Real Analysis - Part 14 - Heine-Borel theorem

Real Analysis - Part 15 - Series - Introduction

Real Analysis - Part 16 - Geometric Series and Harmonic Series

Real Analysis - Part 17 - Cauchy Criterion

Real Analysis - Part 18 - Leibniz Criterion

Real Analysis - Part 19 - Comparison Test

Real Analysis - Part 20 - Ratio and Root Test

Real Analysis - Part 21 - Reordering for Series

Real Analysis - Part 22 - Cauchy Product

Real Analysis - Part 23 - Sequence of Functions

Real Analysis - Part 24 - Pointwise Convergence

Real Analysis - Part 25 - Uniform Convergence

Real Analysis - Part 26 - Limits for Functions

Real Analysis - Part 27 - Continuity and Examples

Real Analysis - Part 28 - Epsilon-Delta Definition

Real Analysis - Part 29 - Combination of Continuous Functions

Real Analysis - Part 30 - Continuous Images of Compact Sets are Compact

Real Analysis - Part 31 - Uniform Limits of Continuous Functions are Continuous

Real Analysis - Part 32 - Intermediate Value Theorem

Real Analysis - Part 33 - Some Continuous Functions

Real Analysis - Part 34 - Differentiability

Real Analysis - Part 35 - Properties for Derivatives

Real Analysis - Part 36 - Chain Rule

Real Analysis - Part 37 - Uniform Convergence for Differentiable Functions

Real Analysis - Part 38 - Examples of Derivatives and Power Series

Real Analysis - Part 39 - Derivatives of Inverse Functions

Real Analysis - Part 40 - Local Extrema and Rolle's Theorem

Real Analysis - Part 41 - Mean Value Theorem

Real Analysis - Part 42 - L'Hôpital's Rule

Real Analysis - Part 43 - Other L'Hôpital's Rules

Real Analysis - Part 44 - Higher Derivatives

Real Analysis - Part 45 - Taylor's Theorem

Real Analysis - Part 46 - Application for Taylor's Theorem

Real Analysis - Part 47 - Proof of Taylor's Theorem

Real Analysis - Part 48 - Riemann Integral - Partitions

Real Analysis - Part 49 - Riemann Integral for Step Functions

Real Analysis - Part 50 - Properties of the Riemann Integral for Step Functions

Real Analysis - Part 51 - Riemann Integral - Definition

Real Analysis - Part 52 - Riemann Integral - Examples

Real Analysis - Part 53 - Riemann Integral - Properties

Real Analysis - Part 54 - First Fundamental Theorem of Calculus

Real Analysis - Part 55 - Second Fundamental Theorem of Calculus

Real Analysis - Part 56 - Proof of the Fundamental Theorem of Calculus

Real Analysis - Part 57 - Integration by Substitution

Real Analysis - Part 58 - Integration by Parts

Real Analysis - Part 59 - Integration by Partial Fraction Decomposition

Real Analysis - Part 60 - Integrals on Unbounded Domains

Real Analysis - Part 61 - Comparison Test for Integrals

Real Analysis - Part 62 - Integral Test for Series

Real Analysis - Part 63 - Improper Riemann-Integrals for Unbounded Functions

Real Analysis - Part 64 - Cauchy Principal Value

Description:

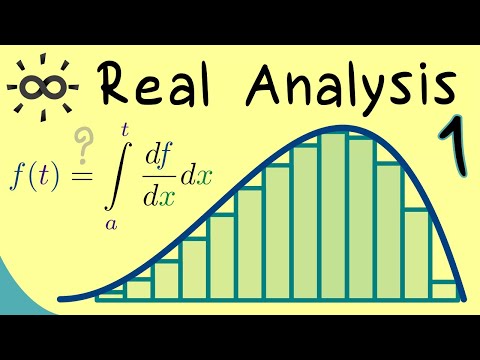
Dive into a comprehensive 10-hour video course on Real Analysis, covering fundamental concepts from sequences and limits to advanced topics like the Riemann Integral and Cauchy Principal Value. Begin with an introduction to Real Analysis, then progress through key theorems including Bolzano-Weierstrass, Heine-Borel, and Taylor's Theorem. Explore series, convergence, continuity, differentiability, and integration, with practical examples and proofs throughout. Master essential mathematical techniques such as the Epsilon-Delta definition, L'Hôpital's Rule, and both Fundamental Theorems of Calculus. Gain a deep understanding of open, closed, and compact sets, as well as various integration methods including substitution, partial fractions, and integration by parts. Conclude with an examination of improper Riemann-Integrals and the Cauchy Principal Value, providing a thorough foundation in Real Analysis principles and applications.

Real Analysis

The Bright Side of Mathematics

Add to list

#Mathematics #Calculus #Mathematical Analysis #Differentiability #Real Analysis #Cauchy Sequences