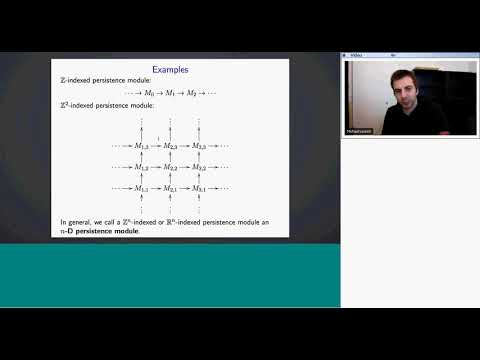
Explore the algebraic stability of zigzag persistence modules in this comprehensive lecture by Michael Lesnick. Delve into key concepts including persistence modules, interval decomposable modules, and the Cross-Smith Theorem. Examine examples, applications, and advanced topics such as block blocks, opposite processes, and index persons modules. Investigate level sets, index modules, bottleneck systems, persistence diagrams, and candy bar codes. Learn about the algebraic stability theorem and its implications for multidimensional stability. Engage with quizzes on matching between barcodes and dimensional bottleneck distance. Conclude with an exploration of the Block Italy Theorem and its relevance to algebraic stability in topological data analysis.