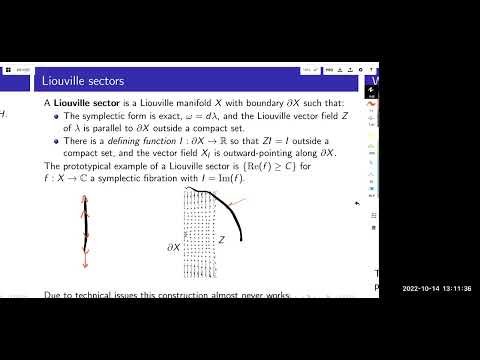
Explore a lecture on functoriality for Fukaya categories of very affine hypersurfaces presented by Maxim Jeffs from Harvard at the Western Hemisphere Virtual Symplectic Seminar. Delve into the intricate relationship between the (partially) wrapped Fukaya categories of a very affine hypersurface and its complement. Examine Auroux's sketched definitions of acceleration and restriction functors, and learn how these can be defined using gluings of Liouville sectors. Discover how this approach supports Auroux's conjectures about mirror counterparts, building on Gammage-Shende's work. Investigate the different realizations of the complement and their impact on Fukaya categories, connected by a non-geometric equivalence through derived Knorrer periodicity. Engage with audience questions addressing topics such as infinity directions, end singularities, restriction functors, and the necessity of derived schemes in relation to η_∞-grading.