Play all

Integrals of trig functions and reduction formulae

Integration by trig substitution and partial fractions

Integration + Partial Fractions

Integration via substitutions.

Separable Differential Equations

Linear and Exact Differential Equations

Homogeneous first order ordinary differential equation

Mixing problems and differential equations.

How to solve 2nd order differential equations

2nd order ODE with constant coefficients: simple method of solution

2nd order ODE with constant coeffcients: non-standard method of solution

Solution to a 2nd order, linear homogeneous ODE with repeated roots

How to solve second order differential equations

Integration and differential equations

Sequences and their limits

What is a Taylor polynomial?

Limit of a sequence

Limit of a sequence: L'Hopital's rule applied to $(\ln n)/n$

Limit of a sequence: $n--$th root of $n^2$

Intro to series + the integral test

Series, comparison + ratio tests

Alternating series and absolute convergence

What is a Taylor series?

What is a power series?

How to calculate power series: a tutorial

Partial derivatives and error estimation

Gradient and directional derivative

Gradient & directional derivative tutorial

Tangent plane approximation and error estimation

Tutorial on gradient and tangent plane

Multivariable Taylor Polynomials

Taylor polynomials: functions of two variables

Critical points of functions

How to find critical points of functions

Second derivative test: two variables

Critical points + 2nd derivative test: Multivariable calculus

How to find and classify critical points of functions

Max / min on closed, bounded sets

Lagrange multipliers

Lagrange multipliers: 2 constraints

Lagrange multipliers example

Method of Lagrange multipliers.

2nd derivative test, max / min and Lagrange multipliers tutorial

Lagrange multipliers: Extreme values of a function subject to a constraint

Intro to double integrals

Double integrals over general regions

Double integral tutorial

Double integrals and area

Double integrals in polar co-ordinates

Reversing order in double integrals

Applications of double integrals.

Double integrals and polar co-ordinates

Double integrals: reversing the order of integration

Tutorial on double integrals

Double integrals: Volume between two surfaces

Centroid + double integral tutorial

Double integrals: Volume of a tetrahedron

Center of mass, double integrals and polar co-ordinates tutorial

Centroid and double integrals

Polar coordinates and double integrals

Reversing order in double integrals

Description:

Explore advanced mathematical concepts essential for finance and actuarial studies in this comprehensive course. Delve into complex integration techniques, differential equations, sequences and series, multivariable calculus, and double integrals. Master integration methods including trigonometric functions, partial fractions, and substitutions. Solve various types of differential equations, from first-order to second-order with constant coefficients. Investigate sequences, limits, and series, including Taylor and power series. Examine multivariable calculus topics such as partial derivatives, gradients, and critical points. Learn optimization techniques using the second derivative test and Lagrange multipliers. Develop proficiency in double integrals, including applications in polar coordinates and volume calculations. Apply these mathematical tools to solve real-world problems in finance and actuarial science through numerous tutorials and examples.

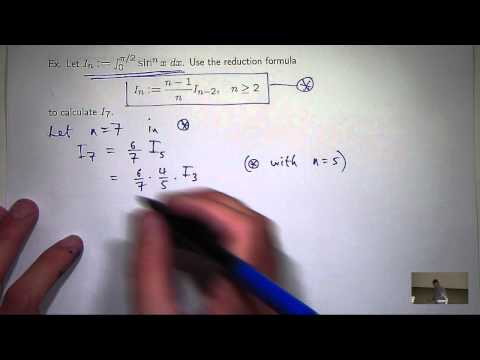
Mathematics for Finance & Actuarial Studies 2

Add to list

#Business #Corporate Governance #Risk Management #Actuarial science #Mathematics #Finance