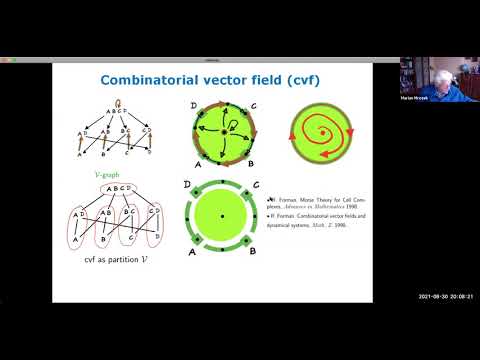
Explore the connections between combinatorial and classical dynamics in this 50-minute lecture on recurrence. Delve into the world of combinatorial dynamical systems, tracing their origins to Robin Forman's 1998 papers and their applications in data science. Discover how combinatorial dynamics offers concise models of dynamical phenomena and learn about topological invariants like the Conley index and Morse decomposition. Examine recent developments in establishing formal ties between combinatorial and classical dynamics, particularly in gradient-like settings. Investigate extensions of these results for recurrent behavior and their potential applications in computer-assisted proofs in dynamics. Cover topics such as combinatorial topology, combinatorial vector fields, admissibility, combinatorial dynamics from flows, and pseudo Morse decompositions. Gain insights into the Van der Pol equations and chaotic isolated invariant sets through practical examples and 3D combinatorial models.