Главная
Study mode:
on
1
Lec01 Introduction to Algebraic Structures Rings and Fields
2
Lec02 Defnition of Vector Spaces
3
Lec03 Examples of Vector Spaces
4
lec04 Defnition of subspaces
5
Lec05 Examples of subspaces
6
Lec06 Examples of subspaces continued
7
Lec07 Sum of subspaces
8
Lec08 System of linear equations
9
lec09 Gauss elimination
10
Lec10 Generating system , linear independence and bases
11
Lec11 Examples of a basis of a vector space
12
Lec12 Review of univariate polynomials
13
Lec13 Examples of univariate polynomials and rational functions
14
Lec14 More examples of a basis of vector spaces
15
Lec15 Vector spaces with finite generating system
16
Lec16 Steinitzs exchange theorem and examples
17
Lec17 Examples of finite dimensional vector spaces
18
Lec18 Dimension formula and its examples
19
Lec19 Existence of a basis
20
Lec20 Existence of a basis continued
21
Lec21 Existence of a basis continued
22
Lec22 Introduction to Linear Maps
23
Lec23 Examples of Linear Maps
24
Lec24 Linear Maps and Bases
25
Lec25 Pigeonhole principle in Linear Algebra
26
Lec26 Interpolation and the rank theorem
27
Lec27 Examples
28
Lec28 Direct sums of vector spaces
29
Lec29 Projections
30
Lec30 Direct sum decomposition of a vector space
31
Lec31 Dimension equality and examples
32
Lec32 Dual spaces
33
Lec33 Dual spaces continued
34
Lec34 Quotient spaces
35
Lec35 Homomorphism theorem of vector spaces
36
Lec36 Isomorphism theorem of vector spaces
37
Lec37 Matrix of a linear map
38
Lec38 Matrix of a linear map continued
39
Lec39 Matrix of a linear map continued
40
Lec40 Change of bases
41
Lec41 Computational rules for matrices
42
Lec42 Rank of a matrix
43
Lec43 Computation of the rank of a matrix
44
Lec44 Elementary matrices
45
Lec45 Elementary operations on matrices
46
Lec46 LR decomposition
47
Lec47 Elementary Divisor Theorem
48
Lec48 Permutation groups
49
Lec49 Canonical cycle decomposition of permutations
50
Lec50 Signature of a permutation
51
Lec51 Introduction to multilinear maps
52
Lec52 Multilinear maps continued
53
Lec53 Introduction to determinants
54
Lec54 Determinants continued
55
Lec55 Computational rules for determinants
56
Lec56 Properties of determinants and adjoint of a matrix
57
Lec57 Adjoint determinant theorem
58
Lec58 The determinant of a linear operator
59
Lec59 Determinants and Volumes
60
Lec60 Determinants and Volumes continued
Description:
COURSE OUTLINE: The main purpose of this course is the study of linear operators on finite dimensional vector spaces. The idea is to emphasize the simple geometric notions common to many parts of mathematics and its applications. Except for an occasional reference to undergraduate mathematics, the course will be self-contained. The algebraic co-ordinate free methods will be adopted throughout the course. These methods are elegant and as elementary as the classical as coordinatized treatment. The scalar field will be arbitrary (even a finite field), however, in the treatment of vector spaces with inner products, special attention will be given to the real and complex cases. Determinants via the theory of multilinear forms. Variety of examples of the important concepts. The exercises will constitute significant asstion ; ranging from routine applications to ones which will extend the very best students.

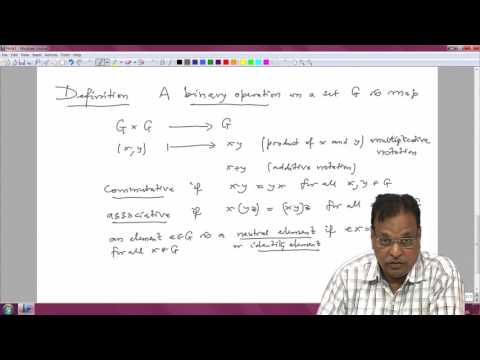
Linear Algebra

NPTEL
Add to list
#Mathematics #Algebra #Linear Algebra #Vector Spaces #Matrices #Linear Transformations #Determinants #Algebraic Structures #Linear Independence #Subspaces
1 of 60

Lec01 Introduction to Algebraic Structures Rings and Fields