Главная
Study mode:
on
1
Intro
2
Motivation
3
Reduced order models
4
Subspace selection Option 1 - by snapshots and SVD-POO
5
When can we expect this to work? For this to be successful there must be some structure to the solution under parameter variation
6
Consider an example
7
A few observations
8
Hamiltonian problems To understand how to address these problems, let us consider Hamitonian problems Equations of evolution
9
Model order reduction Definition: A € R is a symplectic basis transformation
10
Symplectic transformations
11
Model order reduction Suppose for a symplectic subspace
12
The greedy method - algorithm
13
Symplectic Empirical Interpolation Nonlinear case
14
General Hamiltonian problems Now consider the general state dependent Hamiltonian problem
15
Constant degenerate Poisson structure EP
16
Example:The KdV equation
17
State-dependent Poisson structure The complication now is that the Darboux map evolves and is unknown a priori We evolve the map
18
Towards a local basis While the methods work well, the size of the basis is generaly very large This is a classic challenge associated with transport dominated problems which often has a slowly decay…
19
Error estimator To adapt the rank we need to consider two actions Decrease basis size - this is handled by rank condition of 2 and reduction in U Increase basis size - this requires both an error est…
20
Rank adaptation We use as condition for adaptation the growth
21
Example: Shallow water equations
22
Examples Similar example for 2d shallow water equation (26)
23
To summarize cost
24
To summarize The development of reduced order stable methods for time-dependent nonlinear problems is more complex than for traditional reduced models The Hamiltonian model offers access to a number …
25
References
Description:
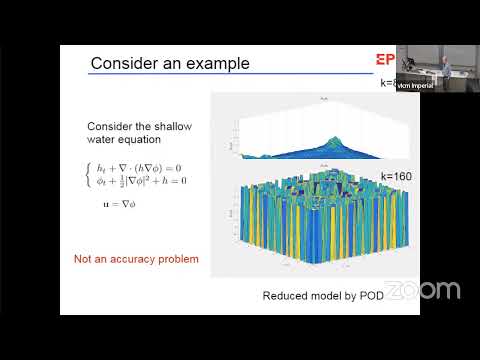
Explore structure-preserving model order reduction techniques for Hamiltonian systems in this 45-minute lecture by Jan S. Hesthaven. Delve into the challenges of developing reduced order models for complex applications, focusing on nonlinear and time-dependent problems. Examine recent developments in projection-based model order reduction methods targeting Hamiltonian problems, which are prevalent in mathematical physics. Learn how approaching the reduction process from the geometric perspective of symplectic manifolds can lead to reduced models that inherit stability and conservation properties. Discover the principles of symplectic geometry, including symplectic vector spaces, Darboux' theorem, and Hamiltonian vector fields. Investigate different structure-preserving reduced basis algorithms and their extensions to problems in noncanonical Hamiltonian form. Explore the development of nonlinear reduced order models using local bases for problems with slowly decaying Kolmogorov n-width, such as transport-dominated problems. Gain insights into the efficiency of these techniques through examples like the Poisson-Vlasov problem in kinetic plasma physics. Read more

Structure-Preserving Model Order Reduction of Hamiltonian Systems

International Mathematical Union
Add to list
#Science #Physics #Classical Mechanics #Hamiltonian Systems #Mathematics #Symplectic Geometry
00:00
-02:27
1 of 25

1 Intro