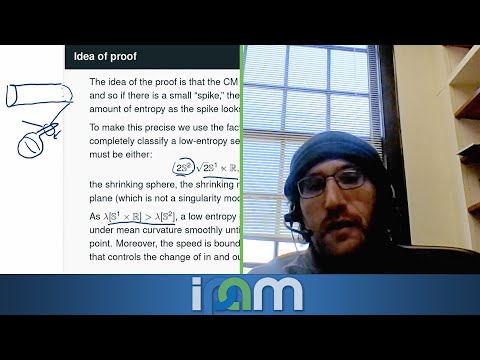
Explore a 24-minute lecture on "Entropy and C^0 stability of hypersurfaces" presented by Jacob Bernstein from Johns Hopkins University at IPAM's Calculus of Variations in Probability and Geometry Workshop. Delve into Colding and Minicozzi's concept of entropy as a measure of submanifold complexity in Euclidean space, and examine how round spheres uniquely minimize this entropy for closed hypersurfaces. Investigate the stability of this rigidity property, focusing on Lu Wang and Bernstein's perspective that demonstrates how closed surfaces in R^3 with entropy close to that of the round two-sphere are similar as closed sets. Discover various generalizations and related questions in this field, covering topics such as sharp inequality, basic properties, nonclosed singularity, quantitative versions, higher dimensions, and thinness.