Главная
Study mode:
on
1
, when changing r to equal 0.69*i, I said "this is what we might think of as (2i)^x", but that is not correct. It's what we'd think of as [Exp(ln(2)*i)]^x for whatever complex number Exp(ln(2)*i) is.
2
Exponential function for i^i
3
Question 1
4
Plug-in imaginary number in exp(x) polynomial
5
Answer 1 and explanation
6
What it really means i^i?
7
e^it as a position vector
8
Question 2
9
Audience question from twitter
10
Answer 2
11
Where you get after traveling π/2 units of time for position vector e^it
12
Question 3
13
Audience tweets
14
Answer 3
15
Question 4
16
Answer 4
17
How exp(rx) or b^x really works?
18
Question 5
19
Audience tweets
20
Answer 5
21
Visualization of f(x)= exp(r*x) i.e. e^(r*x), where r= unique complex number
22
Questions to think about
23
Audience tweets
24
Power tower for i
Description:
Explore the concept of i to the power of i in this comprehensive video lecture from the 3Blue1Brown series. Dive deep into the exponential function for i^i, understand its real meaning, and visualize e^it as a position vector. Learn how to plug imaginary numbers into exponential polynomials and grasp the intricacies of exp(rx) and b^x. Engage with interactive questions, audience tweets, and detailed explanations throughout the session. Discover the visualization of f(x) = exp(r*x) where r is a unique complex number, and ponder thought-provoking questions about power towers for i. Benefit from a structured timeline, beautiful notes by Ngân Vũ, and references to related videos for a thorough understanding of this complex mathematical concept.

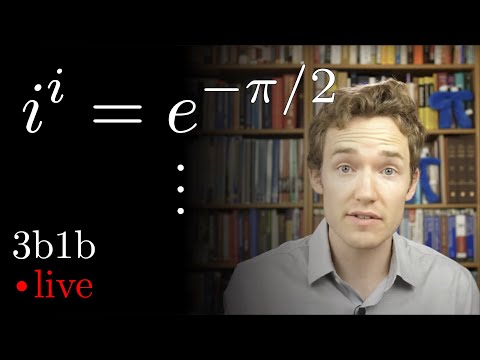
Intuition for i to the Power i - Lockdown Live Math

3Blue1Brown
Add to list
#Mathematics #Complex Numbers #Exponential Functions #Imaginary Numbers
00:00
-00:17
1 of 24

1 , when changing r to equal 0.69*i, I said "this is what we might think of as (2i)^x", but that is not correct. It's what we'd think of as [Exp(ln(2)*i)]^x for whatever complex number Exp(ln(2)*i) is.