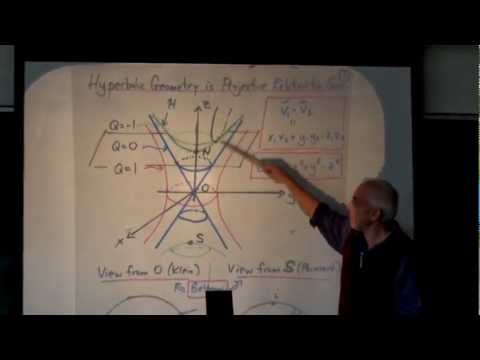
Explore a full lecture on Hyperbolic Geometry as Projective Relativistic Geometry. Delve into three-dimensional relativistic space, examining its quadratic and bilinear forms, with a focus on the upper sheet of the two-sheeted hyperbola. Discover how the Poincaré and Klein models emerge from different perspectives, and learn about the extension to the entire projective plane. Investigate related projective geometry concepts, including harmonic ranges and cross ratios. Examine key metrical notions of quadrance and spread, visualize circles through diagrams, and connect classical distance and angle concepts. Study the main laws of trigonometry and important secondary results like the Parallax theorem. Uncover the Null perspective theorem, null trigonometric results, the 48/64 theorem, and conclude with the fascinating Jumping Jack theorem.