Description:
Explore a 51-minute conference talk on parallel decomposition of persistence modules through interval bases. Delve into an innovative algorithm for decomposing finite-type persistence modules with field coefficients into interval bases. Discover how this construction yields standard persistence pairs in Topological Data Analysis (TDA) and generates special sets inducing interval decomposition. Learn about the distributed computation of this basis across persistence module steps and its applicability to general persistence modules on fields. Examine a parallel algorithm for building persistent homology modules using Hodge decomposition, highlighting the connection between TDA and the Hodge Laplacian. Follow the presentation's structure, covering the introduction, main theorem, graphical representations, key points, harmonics, and comparisons with other approaches. Gain insights into parameterized vector spaces and the potential implications for future research in applied algebraic topology.
Read more
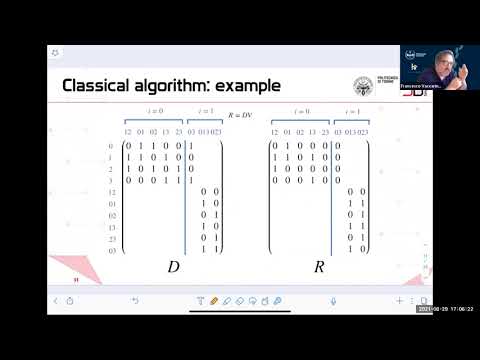
Parallel Decomposition of Persistence Modules Through Interval Bases
Add to list
#Programming
#Programming Languages
#Java
#Hibernate
#Persistence Modules
#Computer Science
#High Performance Computing
#Parallel Computing
#Parallel Algorithms
#Mathematics
#Computational Mathematics
#Geometry
#Topology
#Algebraic Topology
#Data Science
#Topological Data Analysis
#Persistent Homology