Description:
Explore limit theorems in topological data analysis through this 58-minute lecture by Christian Lehn. Delve into the generalization of barcodes and their application in proving limit theorems for point clouds sampled from unknown distributions. Examine the concept of expectation in random barcodes for fixed point sets, and discover precise asymptotics for uniform distributions on compact submanifolds of R^d. Cover key topics including persistent homology, persistence modules, interval modules, bottleneck metric, barcode maps, random persistence modules, convergence proofs, and continuous maps. Gain insights into this collaborative work with S. Kališnik Verošek and V. Limic, expanding your understanding of advanced concepts in topological data analysis.
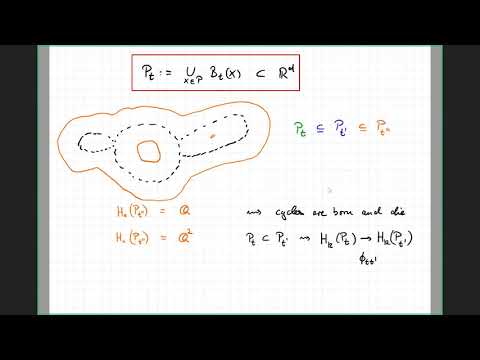
Limit Theorems in Topological Data Analysis
Add to list
#Data Science
#Topological Data Analysis
#Mathematics
#Statistics & Probability
#Probability Theory
#Limit theorems
#Persistent Homology
#Programming
#Programming Languages
#Java
#Hibernate
#Persistence Modules