Description:
Explore a lecture on element-connectivity preserving graph simplification, focusing on a crucial reduction step that maintains element-connectivity in network design and routing problems. Delve into new proofs using setpairs and discover algorithmic advancements for basic element-connectivity problems. Learn about the application of submodularity properties to develop faster algorithms and gain insight into open problems in the field. Examine topics such as packing Steiner trees and forests, internally node-disjoint Steiner trees, and the Cheriyan-Salavatipour Algorithm. Investigate algorithmic aspects, including single pair, all-pair, and global connectivity, as well as approximation techniques in this comprehensive exploration of graph theory and combinatorial optimization.
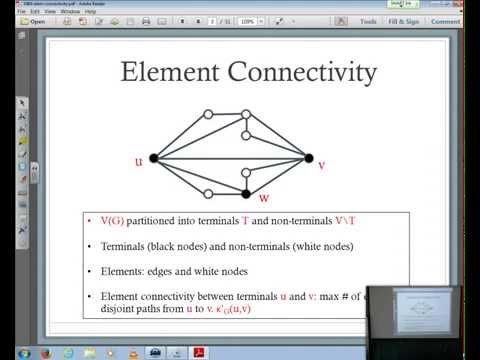
On Element Connectivity Preserving Graph Simplification
Add to list
#Mathematics
#Combinatorial Optimization
#Computer Science
#Computer Networking
#Network Design
#Algorithms
#Approximation Algorithms