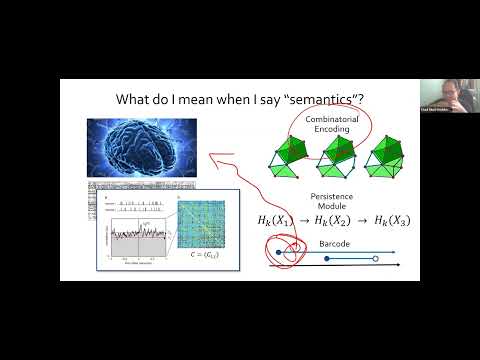
Explore an approach to assigning semantics to persistent homology classes in this 50-minute lecture by Chad Giusti. Delve into the complexities of interpreting "holes" in applied settings, addressing the challenges faced when traditional homology class analysis tools are inaccessible. Learn about a rigorous method that utilizes measurements of observed systems against models or better-understood systems. Discover how this approach, developed in collaboration with Iris Yoon and Robert Ghrist, offers a solution to the semantic interpretation problem in persistent homology. Gain insights into the lecture's structure, covering topics such as the definition of semantics in this context, challenges in practical applications, and the introduction of a new filtration method. Conclude with a summary and information on where to find additional details and code for further exploration.