Description:
Embark on a comprehensive journey through multivariable calculus with this full course playlist, covering essential topics from vectors and curves to partial derivatives and multiple integrals. Develop a strong geometric and conceptual understanding of calculus in three dimensions, following the MATH200 curriculum taught by Dr. Trefor Bazett at the University of Victoria. Explore vector operations, lines, and planes before delving into vector-valued functions, learning to plot curves, calculate tangents, curvature, and arclength. Master partial derivatives and their applications in optimization problems, including the use of Lagrange multipliers. Conclude with an in-depth study of integration techniques, from double and triple integrals to polar and spherical coordinates, and the change of variables theorem using the Jacobian. Throughout the 5-hour course, engage with clear explanations and practical examples that illuminate the big ideas of multivariable calculus, preparing you for advanced mathematical concepts and real-world applications.
Read more
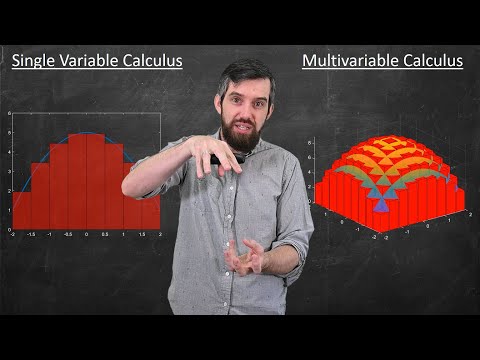
Calculus III - Multivariable Calculus - Vectors, Curves, Partial Derivatives, Multiple Integrals, Optimization
Add to list
#Mathematics
#Calculus
#Multivariable Calculus
#Algebra
#Linear Algebra
#Vectors
#Partial Derivatives
#Geometry
#Curvature