Главная
Study mode:
on
1
Welcome to Calculus II
2
Intro to Integration By Parts --- Examples: ∫xsinxdx & ∫arctan(x)dx
3
Two Tricky Integration By Parts Examples
4
Trigonometric Integrals --- ∫sin^n(x)cos^m(x)dx via Pythagorean or Half-Angle Identities
5
Intro to Trigonometric Substitution --- Ex: Deriving Area of Circle Formula
6
Trig Subs | How To Choose The Substitution & Deal With Indefinite Integrals
7
Deconstructing a messy integral | Trig subs & u-subs combined
8
Integration by Partial Fractions | Big Idea + First Example
9
Partial Fractions | Repeating and irreducible Quadratic Terms
10
Choosing what integration methods to use - Part I
11
Choosing what integration methods to use - Challenging Example!
12
MATH PROF vs TRICKY INTEGRALS
13
Improper Integrals: How to Integrate with Infinities, 2 ways!
14
Comparison Test for Improper Integrals
15
Arclength Formula | Derivation & Ex: Circumference of a Circle
16
Area of Surfaces of Revolution | Derivation & Example
17
Infinite Surface Area but Finite Volume!?!? *Gabriel's Horn*
18
Intro to Sequences
19
Limits of Sequences, Limit laws & Function Representations
20
The Hierarchy of Big Functions || n^n greater than n! greater than e^n greater than n^100
21
Intro to Series: What is 1/2+1/4+1/8+1/16+...?
22
Geometric Series | Convergence, Derivation, and Example
23
Harmonic Series | It diverges, but insanely slowly!
24
Integral Test | Derivation & 1st Example
25
Estimating the Remainder of a Series Approximation via the Integral Test
26
Comparison Test for Series
27
Limit Comparison Test for Series
28
Alternating Series Test | Intuition, Statement & Example
29
Alternating Series | Estimating the Remainder
30
The bizarre world of INFINITE rearrangements // Riemann Series Theorem
31
Absolute Convergence vs Conditional Convergence vs Convergence
32
Ratio & Root Tests | Geometric Series Generalized
33
Choosing Which Convergence Test to Apply to 8 Series
34
Solving Inequalities with Absolute Values: Ex |x-2| less than 3
35
Power Series & Intervals of Convergence
36
Intro to Taylor Series: Approximations on Steroids
37
3 Applications of Taylor Series: Integrals, Limits, & Series
38
Why Taylor Series actually work: The Taylor Inequality
39
Plotting Parametric Curves
40
Tangents to Parametric Curves | Multiple tangents at the same point!!
41
Area under a Parametric Curve | Formula, Derivation, & Example
42
Arclength of Parametric Curves
43
Intro to Polar Coordinates
44
Sketching Polar Curves
45
Areas in Polar Coordinates
46
Example: Area Inside Polar Curves
47
Why Exponential Growth?? Intro to Separable Differential Equations
48
Defining the Natural Logarithm as an Integral?!?!?
49
Intro to COMPLEX NUMBERS // Motivation, Algebraic Definition & Fundamental Theorem of Algebra Ep. 1
50
The geometric view of COMPLEX NUMBERS
51
The Polar Form of COMPLEX NUMBERS // Finding the nth roots of -1
Description:
Dive into a comprehensive 7-hour Calculus II course covering integration methods, series, parametric and polar coordinates, and vectors. Master integration by parts, trigonometric integrals, and trigonometric substitutions. Explore improper integrals, arc length, and surface area of revolution. Delve into sequences and series, including power series, Taylor series, and convergence tests. Learn about vectors and planes. Tackle challenging examples and gain insights into choosing appropriate integration methods. Understand the hierarchy of big functions, explore the bizarre world of infinite rearrangements, and discover applications of Taylor series. Investigate parametric curves, polar coordinates, and complex numbers. Enhance your mathematical skills with Dr. Trefor Bazett's expert guidance through this extensive Calculus II curriculum.

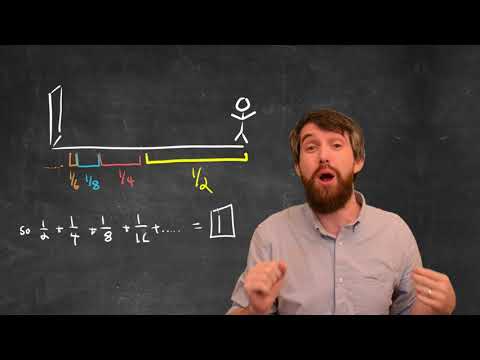
Calculus II - Integration Methods, Series, Parametric-Polar, Vectors

Add to list
#Mathematics #Calculus #Taylor Series #Algebra #Linear Algebra #Vectors #Integration by Parts #Trigonometry #Trigonometric Integrals
1 of 51

Welcome to Calculus II