Главная
Study mode:
on
1
Introduction to Vectors
2
Vector Length and Unit Vectors
3
Dot Product
4
The Two Definitions of Dot Product Are Equivalent
5
Cross Product
6
Jusification of the Properties of Cross Product
7
Cross Product and Areas of Parallelograms
8
More Properties of Cross Product
9
Equations of Lines and Planes in 3-D Space
10
More Examples of Lines and Planes in 3D
11
Parallel and Perpendicular Lines and Planes
12
Distances between Points, Lines, and Planes
13
Vector Functions and Space Curves
14
Closest Point on a Curve
15
Derivatives and Integrals of Vector Functions
16
Arclength of Parametric Curves
17
Functions of Several Variables
18
Limits of Functions of Several Variables
19
Proof that sin x is smaller in magnitude than x.
20
Tricky Limit
21
Partial Derivatives
22
The Chain Rule for Functions of Several Variables
23
Justification of the Chain Rule
24
Directional Derivatives
25
Tangent Plane
26
Local Max and Min Values for Functions of Two Variables
27
The Second Derivatives Test
28
Proof of the Second Derivatives Test
29
Lagrange Multipliers
30
Double Integrals and Riemann Sums
31
Iterated Integrals
32
Double Integrals Over General Regions
33
Double Integrals in Polar Coordinates
34
Justification of the Area Element when Integrating in Polar Coordinates
35
The Area under the Normal Curve is 1
36
Center of Mass
37
Triple Integrals
38
Triple Integrals in Cylindrical Coordinates
39
Spherical Coordinates
40
Triple Integrals in Spherical Coordinates
41
Vector Fields
42
Line Integrals with respect to Arclength
43
Line Integrals in Terms of Riemann Sums
44
Line Integrals with Respect to x and y
45
Line Integrals and Parametrizations
46
Simple Closed Curves - Definitions
47
Types of Regions of the Plane - Definitions
48
Conservative Vector Fields and Independence of Path
49
Green’s Theorem
50
Proof of Green’s Theorem
51
Parametric Surfaces
52
Surface Area of Parametric Surfaces
53
Divergence
54
Curl
Description:
Dive into advanced calculus concepts through a comprehensive 9-hour exploration of multivariable calculus and vector analysis. Begin with an introduction to vectors, covering vector operations, dot and cross products, and their properties. Progress to studying lines and planes in 3D space, including equations, parallelism, and perpendicularity. Explore vector functions, space curves, and their derivatives and integrals. Delve into functions of several variables, limits, partial derivatives, and optimization techniques. Master double and triple integrals, including applications in polar, cylindrical, and spherical coordinates. Conclude with an examination of vector fields, line integrals, Green's Theorem, and an introduction to divergence and curl. Gain a solid foundation in calculus concepts essential for advanced mathematics, physics, and engineering applications.

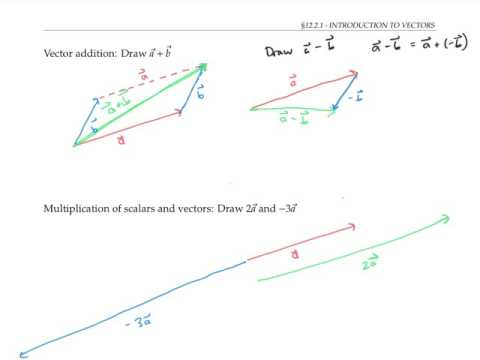
Calculus 3

Add to list
#Mathematics #Calculus #Algebra #Linear Algebra #Vectors #Partial Derivatives #Vector Functions #Vector Calculus #Vector Fields #Lagrange Multipliers #Dot Product #Cross Product
1 of 54

Introduction to Vectors