Description:
Explore the concept of convolution in this 23-minute video that covers its applications in probability, image processing, and Fast Fourier Transforms (FFTs). Dive into discrete convolutions, starting with their role in adding random variables and moving averages. Discover how convolutions are used in image processing techniques and polynomial multiplication. Learn about runtime complexity and how FFTs can speed up convolution operations. Gain insights into the mathematical foundations and practical applications of convolutions, from basic examples to advanced algorithms used in various fields of mathematics and computer science.
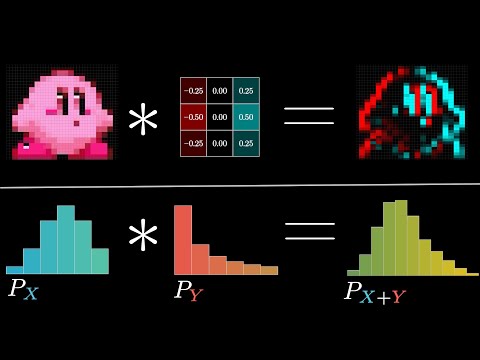
But What Is a Convolution?
Add to list
#Mathematics
#Computer Science
#Data Science
#Artificial Intelligence
#Computer Vision
#Image Processing
#Statistics & Probability
#Probability
#Engineering
#Electrical Engineering
#Signal Processing
#Fast Fourier Transform
#Moving Average