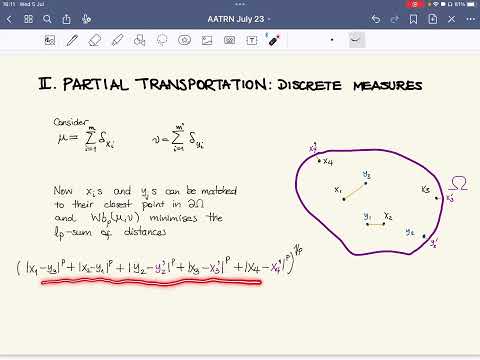
Explore a 31-minute conference talk on bi-Lipschitz embeddings of the space of persistence barcodes presented by Ana Lucía García Pulido for the Applied Algebraic Topology Network. Delve into the concept of optimal partial transport and its application in comparing measures with different total masses. Learn about Figalli and Gigli's metric for measures on Ω⊂ℝⁿ, which allows mass creation or destruction through transportation to or from ∂Ω. Discover the main results concerning bi-Lipschitz embeddability of unordered m-tuples in Wb(Ω) into Hilbert space, with a focus on how the space of persistence barcodes with at most m points bi-Lipschitz embeds into Hilbert space. Gain insights into this collaborative research work with David Bate, expanding your understanding of advanced concepts in algebraic topology and measure theory.