Description:
Dive into the third lecture of a comprehensive series on interior point methods (IPMs) for discrete optimization. Explore the pivotal role of IPMs in recent algorithmic advances, including their application to maximum flow, bipartite matching, linear programming, and geometric median problems. Learn about the theory behind IPMs and their potential for achieving nearly-linear runtimes in various settings. Gain insights into additional properties, key lemmas, minimum cost flow, weighted log barriers, and the concept of Lewis weight barriers. Understand the importance of leverage scores and root deiteration in the context of IPMs. This rigorous introduction provides a thorough overview of the state-of-the-art in IPM theory and its applications to discrete optimization problems.
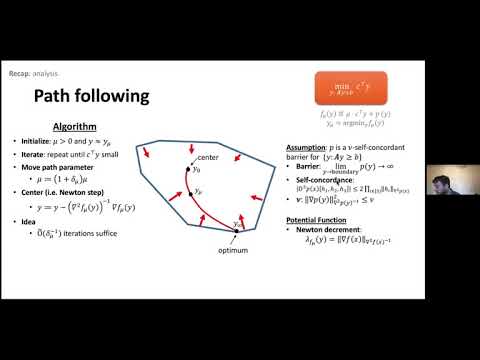
Aaron Sidford- Introduction to Interior Point Methods for Discrete Optimization, Lecture III
Add to list
#Computer Science
#Algorithms
#Optimization Algorithms
#Interior-Point Methods
#Mathematics
#Discrete Mathematics
#Discrete Optimization