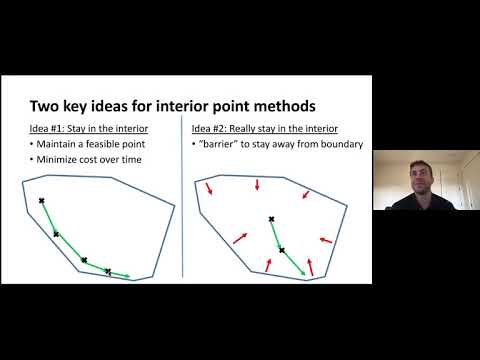
Dive into the second lecture of a comprehensive series on interior point methods (IPMs) for discrete optimization. Explore the pivotal role IPMs have played in recent algorithmic advances, leading to improved running times for various continuous and combinatorial optimization problems. Gain a rigorous introduction to IPM theory, survey recent developments, and examine the state-of-the-art in the field. Delve into specific improvements related to discrete optimization, covering topics such as path following methods, minimizers, Newton's method, and modifications. Investigate primal methods, self-concordance, logarithmic barriers, linear programming, and extended reels. Enhance your understanding of how IPMs have contributed to nearly-linear runtimes in broad settings, including maximum flow, bipartite matching, and geometric median problems.