Description:
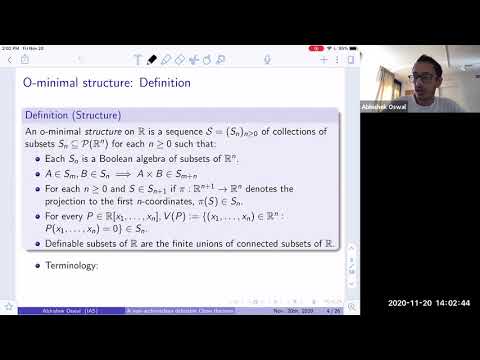
Explore a 45-minute lecture on the non-Archimedean definable Chow theorem, delivered by Abhishek Oswal from the Institute for Advanced Study. Delve into the world of algebraization theorems from o-minimality and their applications in Diophantine geometry and Hodge theory. Examine the definable Chow theorem by Peterzil and Starchenko, which states that closed analytic subsets of complex algebraic varieties, definable in an o-minimal structure, are algebraic subsets. Investigate the non-Archimedean analogue of this result, covering topics such as tame properties of o-minimal structures, p-adic semi-algebraic and subanalytic sets, rationality of Poincaré series, and non-Archimedean analytic geometry. Learn about tame structures, dimension theory, and the rigid subanalytic Riemann extension theorem. Conclude with a proof of a special case of the non-Archimedean definable Chow theorem.
A Non-Archimedean Definable Chow Theorem
Add to list
#Mathematics
#Algebraic Geometry
#Algebra
#Linear Algebra
#Dimension Theory
#Hodge Theory
#Mathematical logic
#O-minimal Structures