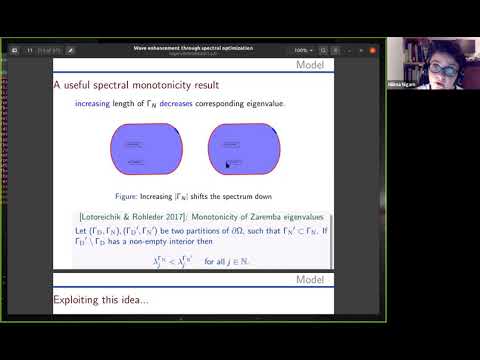
Explore wave enhancement techniques through spectral optimization in this 57-minute virtual seminar presented by Nilima Nigam from Simon Fraser University. Delve into an efficient approach for optimizing transmission signals between two points in a cavity at a given frequency by altering boundary conditions from Dirichlet to Neumann. Learn about the monotonicity of eigenvalues in mixed boundary value problems and the sensitivity of Green's function to small boundary condition changes. Discover highly accurate calculation methods for mixed Dirichlet-Neumann eigenvalues using a layer potential approach. Gain insights into metamaterial resonators, visualization techniques, and the oneshot optimization approach. Examine spectral characterization, boundary integral methods, and asymptotic expansions. Explore practical applications through examples involving kite-shaped domains and higher frequency domains.