Description:
Explore the intricate world of cubic fourfolds and their involutions in this 33-minute lecture by Lisa Marquand from Stony Brook University. Delve into advanced mathematical concepts such as hyperkähler manifolds, lattice notation, and period domains. Examine the Strong Global Twilight Theorem and its implications for the evolution of cubic fourfolds. Investigate the geometry of these complex structures, focusing on antisynthetic and antisymplastic evolutions. Analyze the rationality of cubic fourfolds and engage with thought-provoking questions in this comprehensive exploration of high-dimensional algebraic geometry.
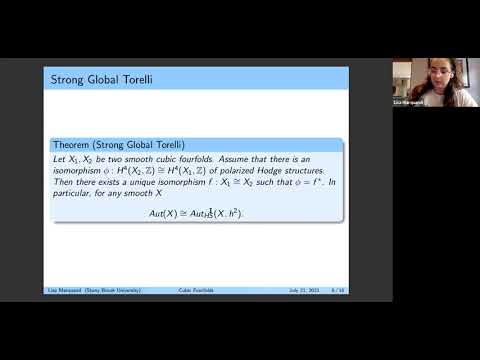
Involutions of a Cubic Fourfold
Add to list
#Mathematics
#Algebraic Geometry
#Geometry
#Computer Science
#Cryptography
#Lattices
#Differential Geometry
#Hyperkähler Manifolds
0:00 / 0:00