Play all

Real Analysis | The Supremum and Completeness of ℝ

Real Analysis | The density of Q and other consequences of the Axiom of Completeness.

Real Analysis | Equinumerosity

Real Analysis | The countability of the rational numbers.

Real Analysis | The uncountability of ℝ

Real Analysis | ℝ and P(ℕ)

Real Analysis | Sequences and the ε-N definition of convergence.

Real Analysis| Three limits of sequences by the definition.

Real Analysis | A convergent sequence is bounded.

Real Analysis | Algebraic Properties of Limits

Real Analysis | The monotone sequence theorem.

Real Analysis | Monotone sequence theorem example.

Real Analysis | Monotone sequence theorem example 2.

Real Analysis | A first look at series.

Real Analysis | The Cauchy Condensation Test

A nice limit with a trick.

Real Analysis | Subsequences

Real Analysis | Cauchy Sequences

Real Analysis | Cauchy Criterion for Series

Real Analysis | Proving some series tests.

Real Analysis | Rearrangements of absolutely convergent series.

Real Analysis | Open subsets of ℝ.

Real Analysis | The limit point of a set A⊆ℝ

Real Analysis | Isolated points

Real Analysis | Closed Sets

Real Analysis | The closure of a set.

Real Analysis | Compact set of real numbers.

Real Analysis | Nested compact sets.

Real Analysis | The Heine-Borel Theorem

Real Analysis | If [a,b] is compact so is any closed and bounded set.

Real Analysis | Perfect Sets

Real Analysis | Connected Sets

Real Analysis | Precise definition of a limit.

Real Analysis | Sequential limits in functions.

Real Analysis | Showing a function is (dis)continuous.

Real Analysis | The continuous image of a compact set.

Real Analysis | Intro to uniform continuity.

Real Analysis | Showing a function is not uniformly continuous.

Real Analysis | Uniform continuity and compact sets.

Real Analysis | The uniform continuity of sqrt(x).

Real Analysis | Topological continuity

Real Analysis | Continuity, connected sets, and the IVT.

Real Analysis | Introduction to differentiability.

Real Analysis | Derivative Rules

Real Analysis | Where are extreme values?

Real Analysis | The Mean Value Theorem

Real Analysis | The Generalized Mean Value Theorem and One part of L'Hospital's rule.

Real Analysis | L'Hospital's Rule (∞/∞ - case)

Real Analysis | Pointwise convergence of sequences of functions.

Real Analysis | Motivating uniform convergence

Real Analysis | Uniform Convergence and Continuity

Real Analysis | Uniform Convergence and Differentiability

Real Analysis | Series of Functions

Real Analysis | Partitions and upper/lower sums.

Real Analysis | Refinements of partitions.

Real Analysis | Riemann Integrability

Real Analysis | An important property of integration.

Real Analysis | Sequences of functions and integration.

Real Analysis | The Fundamental Theorem of Calculus

Real Analysis homework on the Putnam?

Description:

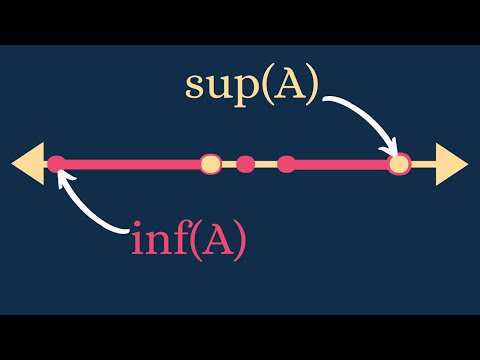
Dive into a comprehensive 15-hour course on Real Analysis, exploring fundamental concepts from the Supremum and Completeness of ℝ to the Fundamental Theorem of Calculus. Master key topics including equinumerosity, countability, sequences, series, limits, continuity, differentiability, and integration. Examine important theorems such as the Monotone Sequence Theorem, Heine-Borel Theorem, and Mean Value Theorem. Develop a deep understanding of topological concepts, uniform convergence, and Riemann integrability. Engage with challenging problems and gain proficiency in proving mathematical statements, preparing you for advanced mathematical analysis and potential Putnam-level problem-solving.

Real Analysis

Add to list

#Mathematics #Mathematical Analysis #Real Analysis #Calculus #Convergence

0:00 / 0:00